Делимся планом урока по физике для учителей по теме «Механические колебания» для учеников 9 класса.
Цели урока:
- Объяснить понятия «устойчивого и неустойчивого равновесия».
- Вспомнить определения: «сила тяжести», «сила упругости», «сила натяжения нити».
- Провести простой эксперимент и почувствовать особенности колебательного движения.
- Дать определение механическим колебаниям.
- Дать определение гармонических колебаний.
- Познакомить учеников с новыми понятиями: «механические колебания», «колебательная система», «положения устойчивого равновесия», «крайние (амплитудные) положение колебательной системы», «свободные и вынужденные колебания», «период», «частота», «амплитуда».
- Определить единицы измерения частоты, циклической частоты и периода колебаний.
- Получить формулы периода колебаний для пружинного и математического маятника.
- Закрепить материал: решить задачи, провести эксперименты с двумя простейшими механическими колебательными системами — пружинным и математическим маятником.
Задачи урока физики:
- Познакомить учащихся с колебательным движением, его особенностями и основными характеристиками, рассмотреть виды колебаний и колебательных систем.
- Формировать логическое мышление учащихся, умение наблюдать и анализировать наблюдаемые явления.
- Способствовать формированию умений к самостоятельной работе и анализу в реальной ситуации.
Содержание:
- Колебательные процессы
- Уравнения гармонических колебаний
- Основные характеристики колебательной системы
- Пружинный маятник. Вывод формулы периода колебаний
- Циклическая (круговая) частота. Период колебаний пружинного и математического маятника
- Решение задач
1. Колебательные процессы. Устойчивое и неустойчивое положение тела. Условия, необходимые для наличия колебаний
В окружающем нас мире постоянно происходят периодические (или почти периодические) процессы, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Для того чтобы колебания могли происходить, необходимо два условия: наличие устойчивого положения равновесия и силы, которая бы возвращала все в положение равновесия.
Если сделать это не получится — просто убедитесь, что даже самое маленькое усилие, сдвигающее шарик из положения равновесия, приведет к его скатыванию с чашки. Такое положение шарика называется неустойчивым.
Теперь поставьте чашку на стол обычным способом — дном вниз — и бросьте в нее шарик. После нескольких колебаний шарик остановится на дне чашки. Если толкнуть шарик снова, он опять вернется в «удобное» для него положение. Это положение называется устойчивым.
В первом случае при выведении тела из положения равновесия возникает сила, выводящая тело из положения равновесия, а во втором — возвращающая в положение равновесия. В проведенном эксперименте главную роль играла сила тяжести, а помогала ей сила нормальной реакции опоры.
Теперь представьте ребенка, прыгающего на батуте. В этом процессе задействованы тоже две силы: сила тяжести (она действует на ребенка, направлена вертикально вниз к центру Земли и заставляет его опускаться вниз) и сила упругости (она действует на ребенка и направлена вертикально вверх, когда ребенок находится в нижней точке).
Ответ: сила, о которой забыли сказать, — это вес. Сила, с которой ребенок вследствие притяжения к Земле действует на батут и продавливает его).
Если подвесить небольшое тело на длинной нити и толкнуть его, придав ему горизонтальную скорость, то это тело начнет раскачиваться из стороны в сторону. Ответственными за эти колебания тела будут сила натяжения нити, направленная вдоль нити к точке закрепления нити и сила тяжести, направленная вертикально вниз.
Механическими колебаниями называются периодические (или почти периодические) изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальная энергия и т. п.).
Примерами простых колебательных систем могут служить груз на пружине или математический маятник.

На рисунке слева красными стрелками указаны сила упругости Fупр и сила тяжести mg. На рисунке справа — сила натяжения нити F и сила тяжести mg.
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того как система была выведена из состояния равновесия, а колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.
Вам могут быть интересны и другие наши статьи к урокам физики:
2. Уравнения гармонических колебаний
Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x=f(t).
Самое простое колебательное движение тела — гармоническое колебание. Гармоническим называют колебание, в процессе которого величины, характеризующие движение (смещение, скорость, ускорение и др.), изменяются по закону синуса или косинуса (гармоническому закону). В общем виде этот закон задается формулой:
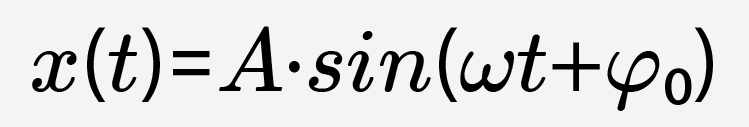 или
или 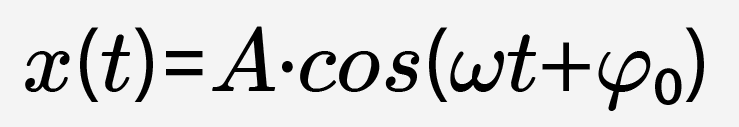
где x(t) — значение изменяющейся величины в момент времени t, A — амплитуда колебаний, 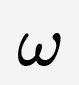 — циклическая (круговая) частота колебаний,
— циклическая (круговая) частота колебаний,  — начальная фаза колебаний.
— начальная фаза колебаний.
Гармонические колебания являются периодическими. Период T этих колебаний равен периоду функции 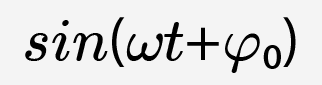 или
или  , то есть:
, то есть:
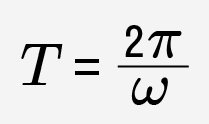
Очень часто как свободные, так и вынужденные колебания в различных механических колебательных системах имеют форму гармонических колебаний.
Глядя на графики функций синуса и косинуса (см. рисунок), видно, что первый график описывает колебания, начинающиеся из положения равновесия, а второй — из точки, максимально удаленной от положения равновесия (амплитудной точки).
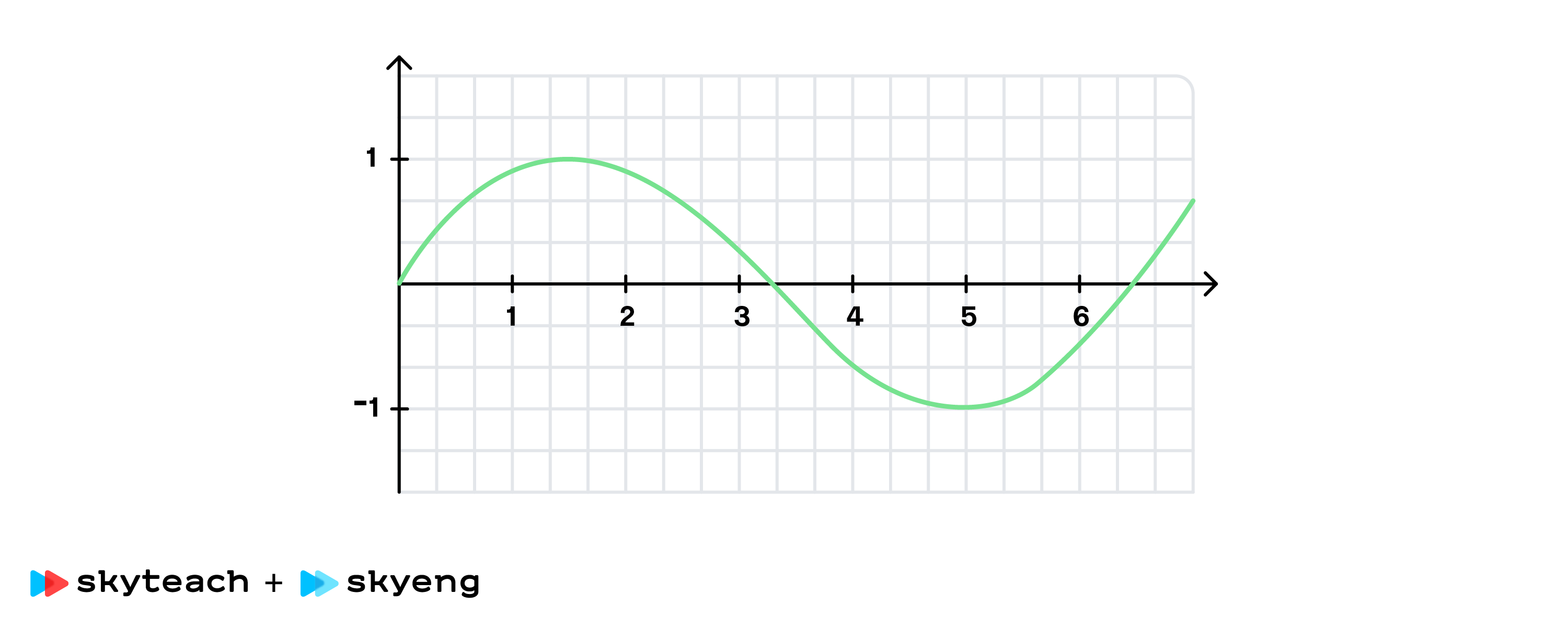

График косинуса будет более близок по смыслу для свободных колебаний. Колебательная система уже выведена из положения равновесия и находится в амплитудном (крайнем) положении и, предоставленная самой себе, начинает совершать колебания.
Слова «колебательная система» мы говорим, когда точно не знаем, о какой именно колеблющейся системе идет речь. Это может быть пружинный маятник, или математический, или вообще какой-то сложный аппарат, совершающий колебания.
3. Основные характеристики колебательной системы
Частота — физическая величина, характеризующая колебательный процесс и показывающая, какое количество колебаний совершается колебательной системой в единицу времени.
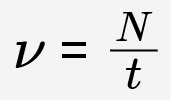 , где N — количество колебаний, t — время, за которое эти колебания совершены.
, где N — количество колебаний, t — время, за которое эти колебания совершены.
Единица измерения частоты в системе СИ — Герц (Гц – сокращенное обозначение).
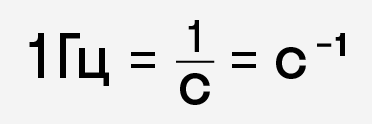
Круговая (циклическая) частота — число колебаний, совершенных колебательной системой за 2п секунд. Единица измерения циклической частоты в системе СИ — с-1.
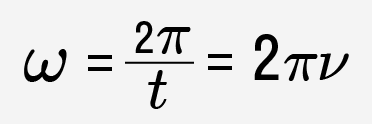
Период колебаний T — время одного полного колебания.
Исходя из этого, частоту колебаний можно записать как одно колебание, происходящее за время, равное периоду колебаний.
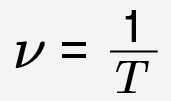
Тогда для периода колебаний можно записать так:
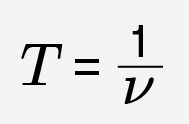 или
или 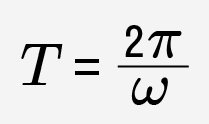
Единица измерения периода T в системе СИ — секунда.
Амплитуда колебаний — это максимальное отклонение колеблющегося тела от положения равновесия.
4. Пружинный маятник. Вывод формулы периода колебаний (на примере пружинного маятника)
Пружинный маятник рассматривают в двух вариациях:
- в виде горизонтальной пружины, прикрепленной одним концом к вертикальной стенке, а другим концом соединена с грузом массы m, который движется без трения по горизонтальной поверхности;
- в виде вертикальной пружины, закрепленной одним концом в какой-то точке, а к другому ее концу подвешен груз массой m.
Груз в таких системах совершает колебания под действием силы упругости пружины, к которой он прикреплен.
Считая эти колебания гармоническими, рассмотрим их особенности в разные моменты времени и опишем, какие значения принимают физические величины: координата, скорость, ускорение, кинетическая и потенциальная энергия.
Изобразим на рисунке колебательную систему, находящуюся в устойчивом равновесии. Выберем ось координат OX, вдоль которой будут происходить колебания. Укажем все силы, действующие на груз, находящийся в состоянии покоя.
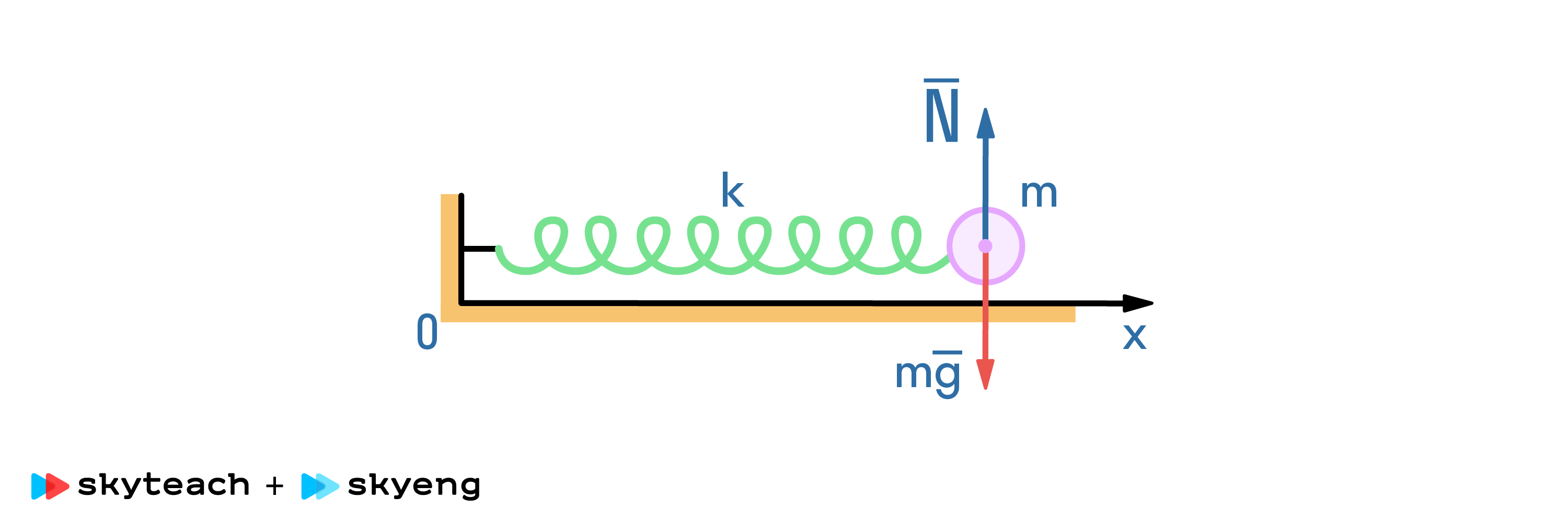
Сила нормальной реакции опоры  и сила тяжести
и сила тяжести 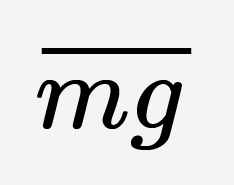 уравновешивают друг друга. Следовательно, ускорение тела равно нулю.
уравновешивают друг друга. Следовательно, ускорение тела равно нулю.

Для вертикального пружинного маятника. Уравновешивающие друг друга силы, это начальная сила упругости, возникшая после прикрепления груза к подвешенной пружине (она же когда-то была нерастянута)  упр0 и сила тяжести
упр0 и сила тяжести 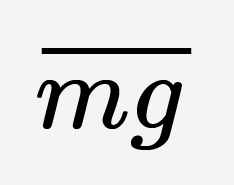 .
.
После того как тело, прикрепленное к пружине, толкнуть в какую-либо сторону вдоль оси OX (т.е. вывести его из положения устойчивого равновесия, сообщив телу кукую-то скорость или передав энергию) оно начнет совершать колебания в окрестности точки, называемой положением равновесия. Положение равновесия — это положение, в котором ускорение тела равно нулю, так как результирующая всех сил, действующих на тело в этой точке, равна нулю. А, поскольку ускорение тела в этой точке равна нулю, то скорость тела будет максимальной.
Предположим, что телу сообщили скорость в направлении увеличения вдоль оси OX. В результате тело сместится на какое-то расстояние x, пружинка растянется на длину x. Со стороны пружины на тело будет действовать сила упругости, равная по модулю k∙x. Вектор этой силы упругости будет направлен в сторону положения равновесия. Легко понять, что возникающая сила будет тормозить тело. Ускорение, действующее на тело, направлено в ту же сторону, что и сила. Скорость тела постепенно будет уменьшатся и рано или поздно станет равной нулю.
Что интересно, эта ситуация противоположна той, которая была в положении равновесия, а именно: там скорость была наибольшей, а ускорение — равно нулю. В амплитудном положении — наоборот: скорость равна нулю, а ускорение — максимально. Это нужно запомнить!
Сперва тело обладало кинетической энергией. В процессе удаления от положения равновесия кинетическая энергия уменьшается, но возрастает потенциальная энергия пружины. В амплитудном положении вся кинетическая энергия перешла в потенциальную.
Далее тело по инерции проходит положение равновесия и начинает отклоняться в противоположную сторону. Пружина начнет сжиматься, сила упругости начнет возрастать и будет направлена снова к положению равновесия, но с другой стороны. Сила упругости будет тормозить тело, и, когда оно отклонится на максимальное расстояние (достигнет амплитудного положения с противоположной стороны), то остановится. Кинетическая энергия тела станет равной нулю, а потенциальная энергия пружины — достигнет максимального значения. Ускорение и сила упругости снова будут максимальными. Ситуация полностью повторилась!
И для завершения колебания тело возвращается в положение равновесия. Всего получается четыре этапа колебания. Такие колебания будут повторяться бесконечно долго, если нет трения.
Время одного полного колебания, то есть время, за которое тело, выйдя из положения равновесия, вернулось туда же, но со скоростью, направленной в ту же сторону и имеющую то же самое значение, называется периодом колебания T.
Наряду с периодом, вводят понятие частоты. Частота — это количество колебаний колебательной системы за единицу времени
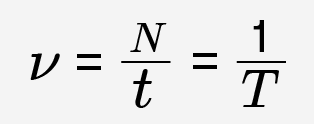 .
.Следующий важный момент — это формула периода колебаний математического маятника. Вывод этой формулы будет уже в одиннадцатом классе, но показать его можно уже сейчас
(для физмат классов и особо интересующихся физикой).
4.1 Вывод формулы периода колебаний (на примере пружинного маятника)
Обратите внимание, что сила упругости направлена всегда в сторону, противоположную смещению тела от положения равновесия. Тогда второй закон Ньютона в проекции на ось OX запишется следующим образом:

На языке математики ускорение называют «второй производной от координаты по времени», а второй закон Ньютона записывают в виде дифференциального уравнения второго порядка:
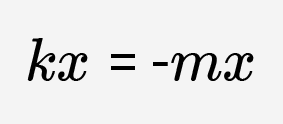 или
или 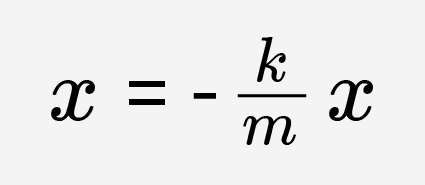
Несмотря на внешнюю сложность и непонятность этого уравнения, его решением является уже известные вам тригонометрические функции:
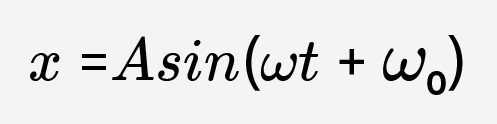 или
или 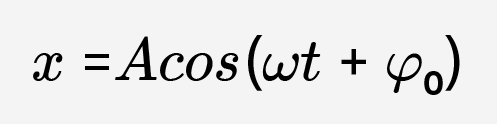
Стоит только заметить, что вторая производная от каждой из этих функций, является той же самой функцией, но взятой с противоположным знаком и умноженной на циклическую частоту в квадрате.
 или
или 
Теперь это дифференциальное уравнение становится не таким уж и непонятным:
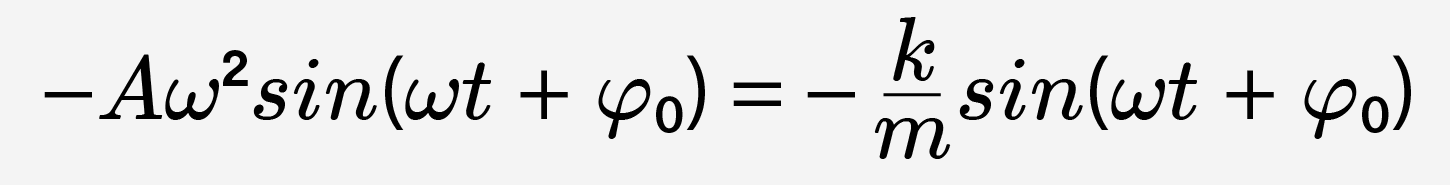 или
или 
5. Циклическая (круговая) частота. Период колебаний пружинного и математического маятника
Циклическая (круговая) частота:
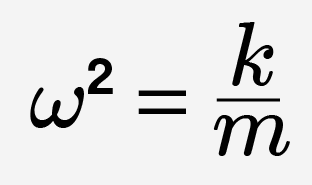 , а
, а 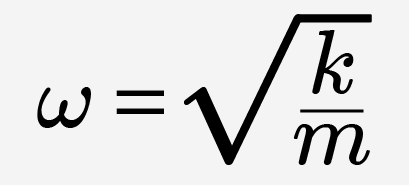
Теперь, вспоминая определение циклической частоты, получаем формулу периода пружинного маятника:
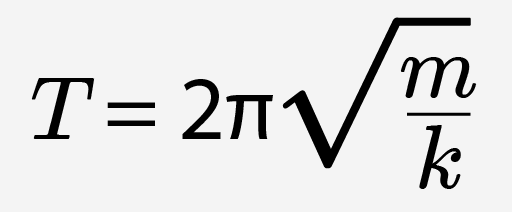
Для колебательной системы (математический маятник) весь процесс абсолютно аналогичен, только силой, возвращающей систему в положение равновесия, будет являться равнодействующая силы натяжения нити и силы тяжести. Превращение энергии, изменение скорости и ускорения колеблющегося тела, изменение координаты тела с течением времени — точно такие же.
Формулы для циклической частоты и периода другие:
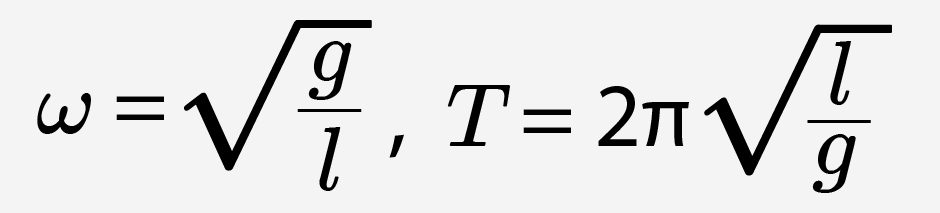
Здесь l — длина нити математического маятника, а g — ускорение свободного падения.
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити длиной l в поле силы тяжести (или других сил).
6. Решение задач
Задачи про «во сколько раз изменится»
Задача. Как изменится циклическая частота пружинного маятника, если массу тела, прикрепленного к пружинке, увеличить/уменьшить в 4,9,16 и т.д. раза?
Решаем методом «стрелочек»: записываем формулу изучаемой величины.
Пририсовываем рядом с изменяющейся величиной: если величина увеличивается – то стрелочку «вверх», если уменьшается – вниз. После этого учитываем то математическое выражение, в котором участвует изменяемая величина и делаем вывод. Например: если масса тела увеличится в 4 раза 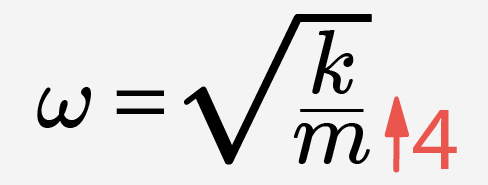 ,то дробь, стоящая под знаком квадратного корня, уменьшается в 4 раза
,то дробь, стоящая под знаком квадратного корня, уменьшается в 4 раза 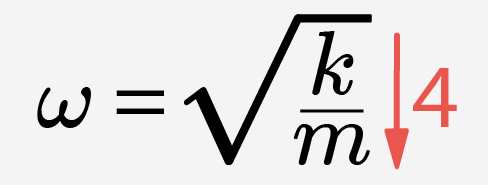 . Следовательно, после извлечения корня, получаем, что циклическая частота уменьшится в 2 раза
. Следовательно, после извлечения корня, получаем, что циклическая частота уменьшится в 2 раза 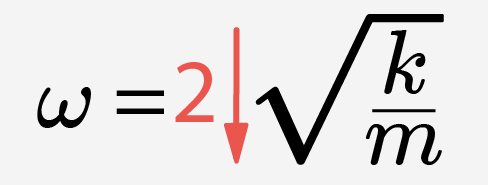 .
.
Задание: придумайте 5 задач такого типа для циклической частоты пружинного и математического маятника.
Например: как изменится период математического маятника, если длина нити маятника будет увеличена в 9 раз, а маятник будет двигаться вверх с ускорением 30 м/с2? 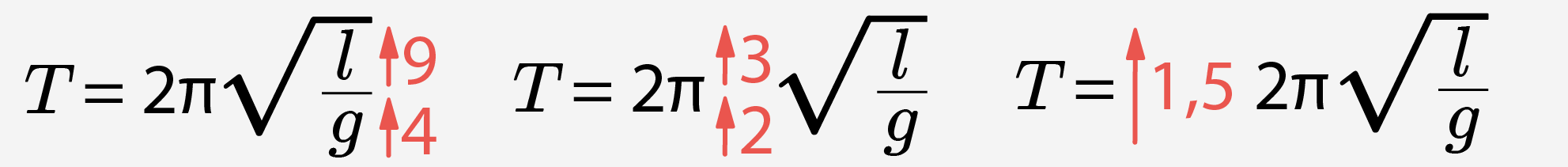 . Период возрастает в 1,5 раза.
. Период возрастает в 1,5 раза.
Задачи на исследование графиков
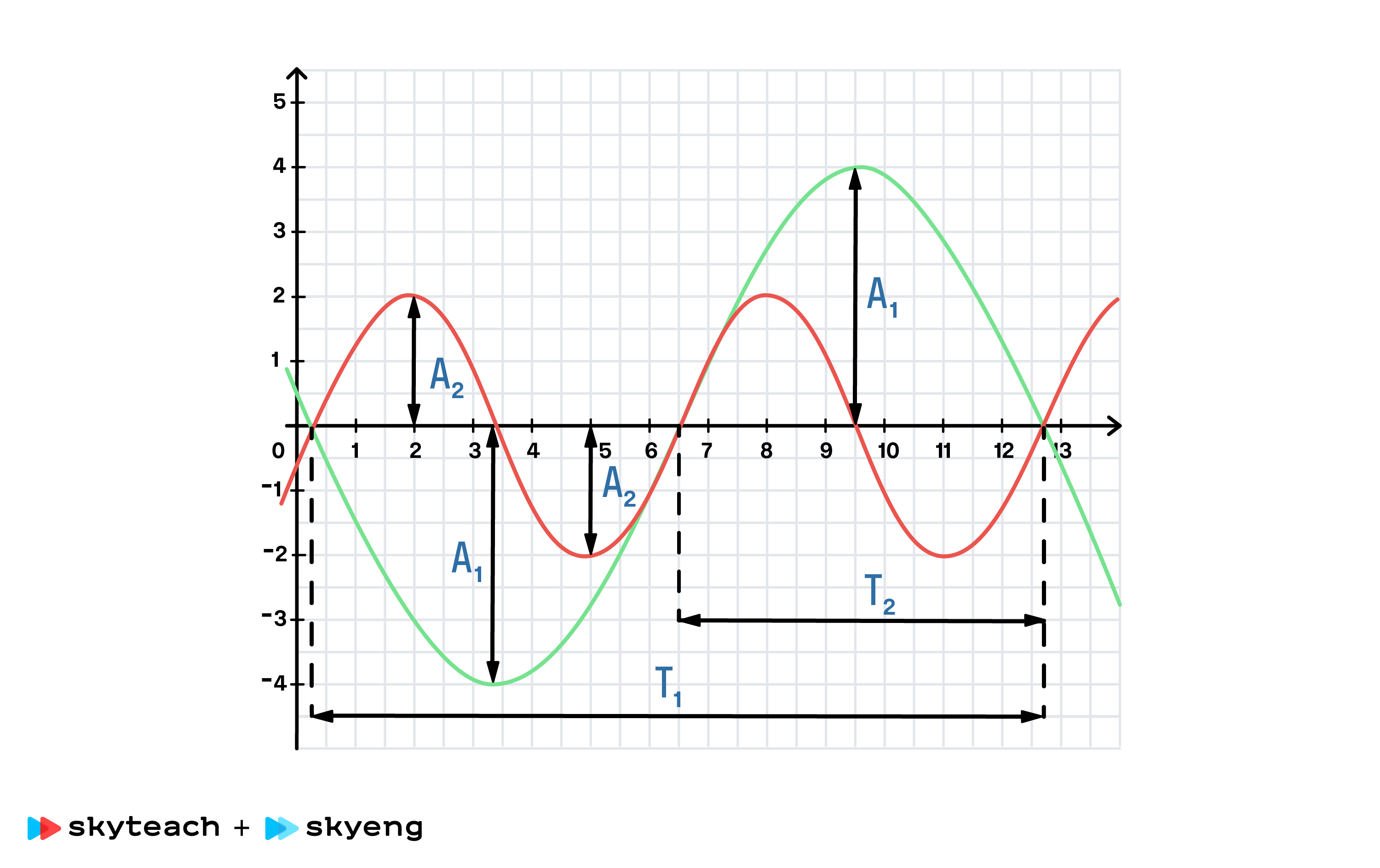
Для успешного решения этих задач надо запомнить, как определить по графику амплитуду и период колебаний. Все остальное определяем по формулам.
Чаще всего эти задачи бывают на сравнение двух графиков, например: сравните амплитуду, период или частоту двух колебаний, представленных двумя разными графиками.
Задачи на дом
Задача 1. Как изменится период свободных колебаний математического маятника, если его переместить на планету, где ускорение свободного падения меньше земного в 2 раза, и увеличить длину нити в 2 раза? Выберите верный вариант ответа:
- увеличится в 8 раз
- увеличится в 2 раза
- уменьшится в 2 раза
- уменьшится в 8 раз
- уменьшится в 64 раза
Задача 2. При свободных колебаниях математического маятника в некоторый момент времени его кинетическая энергия оказалась равной 20 Дж, что было в два раза меньше максимальной потенциальной энергии. Чему равна полная механическая энергия колебаний этого маятника? Ответ выразите в Дж, округлив до целых.
Ответ: 40 Дж
Задача 3. «Колебательное движение задано уравнением 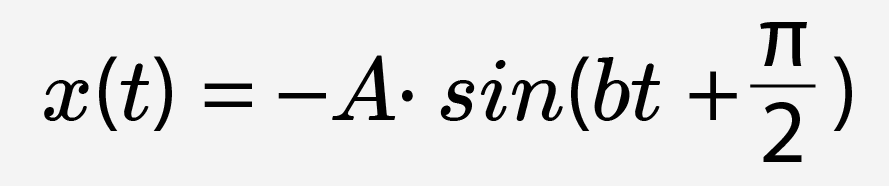 , где A=20 см, b=5с-1. Чему равно максимальное ускорение колеблющегося тела? Ответ дать в
, где A=20 см, b=5с-1. Чему равно максимальное ускорение колеблющегося тела? Ответ дать в  , округлив до целых.»
, округлив до целых.»
Ответ: 
Задача 4. «Брусок массой 200 г совершает гармонические колебания по гладкой
горизонтальной поверхности под действием пружины жесткостью 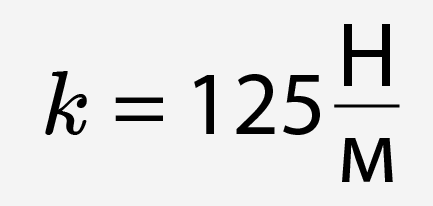 . Определите амплитуду колебаний A, если максимальное значение возвращающей силы (по модулю) в два раза меньше действующей на груз силы тяжести. Ответ выразите в миллиметрах, округлив до целых.»
. Определите амплитуду колебаний A, если максимальное значение возвращающей силы (по модулю) в два раза меньше действующей на груз силы тяжести. Ответ выразите в миллиметрах, округлив до целых.»
Ответ: 8 мм
Задача 5. Груз массой m=400 г совершает гармонические колебания на гладкой
горизонтальной поверхности под действием пружины с жесткостью 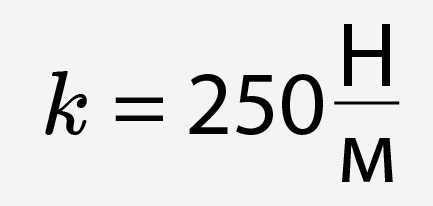 . Амплитуда колебаний A=4 см. Найдите максимальную скорость движения груза. Ответ дайте в метрах в секунду.
. Амплитуда колебаний A=4 см. Найдите максимальную скорость движения груза. Ответ дайте в метрах в секунду.
Ответ: 
Советуем преподавателям физики заглянуть и в эти статьи:

















 Skyteach
Skyteach 
 Анна Михайлова-Левина
Анна Михайлова-Левина 
 Александр Кудрявцев
Александр Кудрявцев