План урока по теме «Основное тригонометрическое тождество»

Тема «Основное тригонометрическое тождество» вызывает у школьников недоумение и страх. 9 из 10 моих учеников во время подготовки к ОГЭ говорили о том, что тема трудная. Этот план урока поможет преподавателям математики зайти в сложную тему с уже известных и сделать синусы и косинусы следствием из знаний по темам «Теорема Пифагора» и «Подобие треугольников». В статье — 13 заданий для практики во время занятия и д/з.

Учите школьников и получайте
от 40 до 100 000 рублей в месяц!

Приглашаем учителей математики
с высшим образованием (или студентов последнего курса) и опытом подготовки
к выпускным экзаменам

Начать преподавать

Содержание:

• Цели урока
• Разминка
• Подводка к теме
• Определения
• Практическая часть
• Первое доказательство
• Практическая часть
• Основное тригонометрическое тождество
• Вывод новых формул
• Итоги урока
• Домашнее задание

Цели урока

1. связать стороны и углы в прямоугольном треугольнике;
2. изучить понятия синуса, косинуса, тангенса и котангенса;
3. научиться применять их на практике;
4. отработать навыки доказательств и вывода формул.

Разминка

Вспомните со школьником основные Пифагоровы тройки.

1. В прямоугольном треугольнике катеты равны 3 и 4. Чему равна гипотенуза?
2. В прямоугольном треугольнике катет равен 5, а гипотенуза — 13. Найдите второй катет.
3. В прямоугольном треугольнике катет равен 40, а гипотенуза — 41. Найдите второй катет.

В задании 2 и 3 используйте формулу разности квадратов, чтобы без сложных вычислений найти неизвестные элементы треугольников.

Сколько платят в Skyeng преподавателю математики?

Из чего складывается доход учителей, рассказываем в специальной статье.

Подробне

Подводка к теме

Перед изучением новой темы «Основное тригонометрическое тождество» актуализируйте знания по теме-предшественнику. Чтобы ввести тригонометрические функции, вспомните с учеником подобие треугольников.

Этапы подготовки:

Шаг 1. Рассмотрите пример двух подобных прямоугольных треугольников.

Шаг 2. Вспомните соотношения между сторонами.

Шаг 3. Докажите, что для подобных треугольников отношения соответствующих сторон равны.

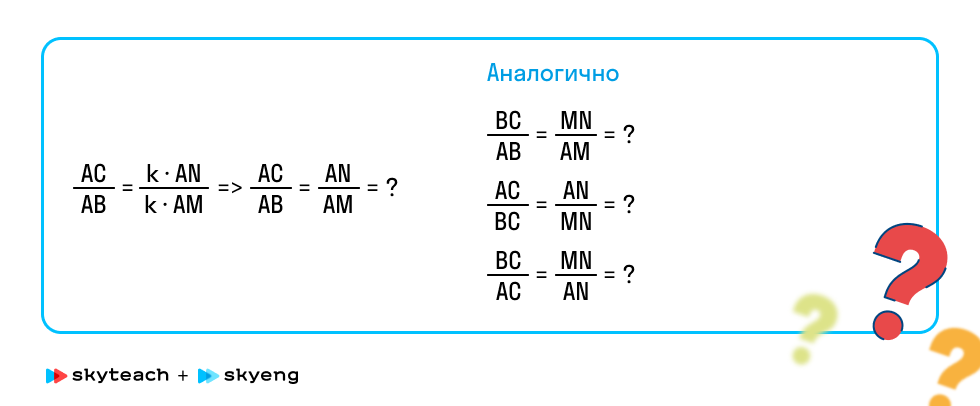
Шаг 4. Обсудите с ребенком следующее: если изменить величину острого угла в прямоугольном треугольнике, изменятся длины сторон и соотношения между ними.

Эксперты Skyeng подготовили
для учителей подарки.

Выбирайте те, что нужны, или заберите все!

Получить подарки

Определения

Соотношения из пункта выше требуют новых обозначений. Здесь на сцену и выходят синусы, косинусы, тангенсы и котангенсы, которые встают на место вопросов.

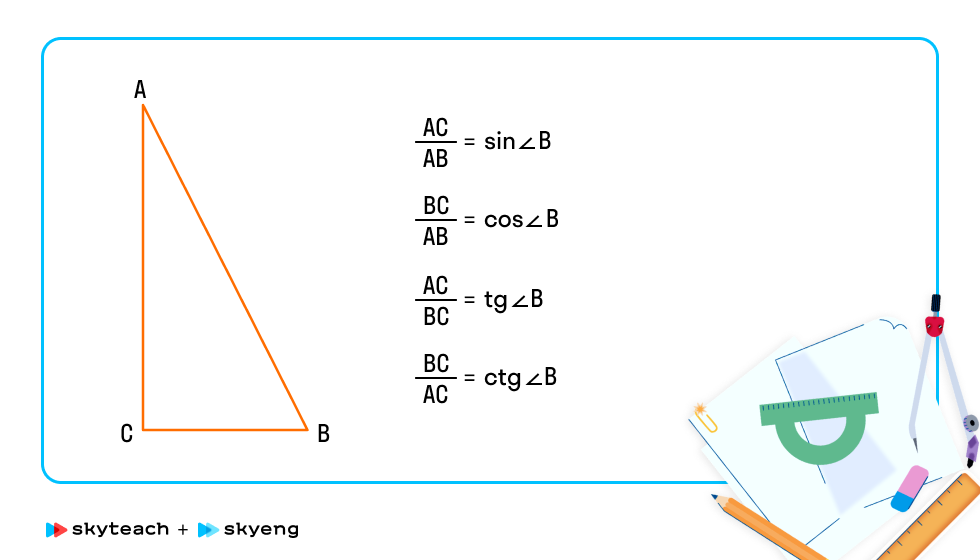
Упражнение. Для того же треугольника записать синус, косинус, тангенс и котангенс угла А.

Практическая часть

Задание 1. Найти тригонометрические функции острых углов в треугольниках со сторонами 3, 4, 5 и 6, 8, 10. 

Выводы из задания 1

1. Треугольники подобны. Значения тригонометрических функций совпадут.
2. Синус одного острого угла будет равен косинусу другого.

Задание 2. Найти пары равных функций.

Задание 3. Найти тригонометрические функции острых углов в треугольнике со сторонами 5, 12, 13.

Первое доказательство

Задание 4.

Практическая часть

Задание 5. Найти синус, косинус, тангенс большего острого угла прямоугольного треугольника с катетами 7 см и 24 см.

Основное тригонометрическое тождество

Школьник уже вспомнил, что длины сторон прямоугольного треугольника связаны теоремой Пифагора. Следовательно, тригонометрические функции тоже взаимосвязаны.

Задание 6. Доказать тождества, используя определения тригонометрических функций и теорему Пифагора.

Задание 7. Найти значения выражений.

sin² 40^° + cos² 40^° = …
cos² 89^° + sin² 89^° = …

Разберите вместе с учащимся следующий пример: в прямоугольном треугольнике АВC с острым углом А известно, что sin угла А = 0,8. Необходимо найти cos угла А.

Решение.

sin² угла А + cos² угла А = 1
cos² угла А = 1 − sin² угла А = 1 − 0,64 = …
cos² угла А = …

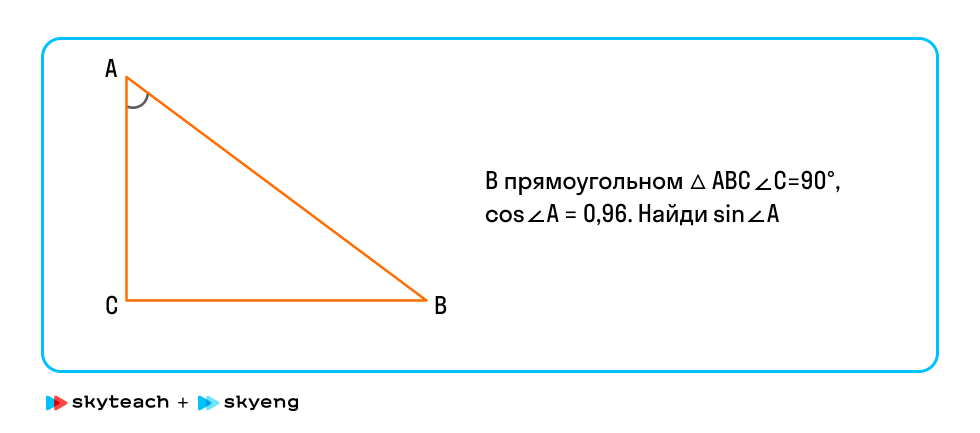
Задание 8. В прямоугольном треугольнике АВC угол С равен 90^°, cos угла А равен 0,96. Нужно найти sin угла А.

Задание 9. Найти котангенс острого угла прямоугольного треугольника, если косинус этого угла равен ³⁄_√10

Задание 10. Гипотенуза прямоугольного треугольника равна 20 см, а косинус одного из острых углов равен 0,8. Нужно найти катеты этого треугольника. Ответ записать в порядке возрастания через точку с запятой.

Топ-5 ошибок в ЕГЭ базового уровня по математике

Стратегия быстрой подготовки к ЕГЭ по математике

Как готовят к ЕГЭ по математике в Skyeng?

ЕГЭ по математике: Координатный метод 

Вывод новых формул

Задание 11. Зная основное тригонометрическое тождество, совместно с учеником докажите следующую формулу.

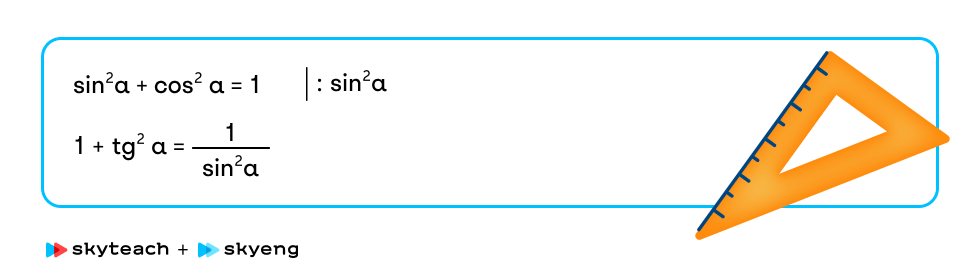
Обсудите с учащимся, зачем эта формула нужна.

Задание 12. Найти синус, косинус и котангенс острого угла прямоугольного треугольника, если тангенс этого угла равен 7. В ответе соотнести значения.

Задание 13.

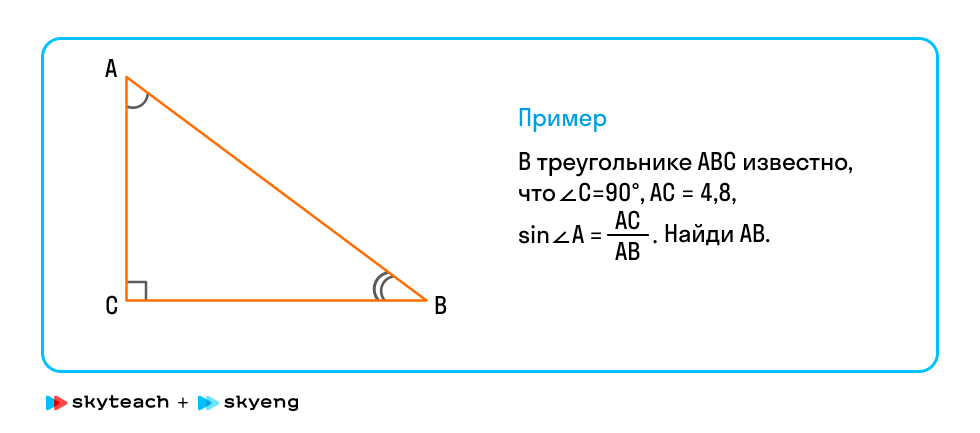
Итоги урока

Во время подведения итогов вспомните цели урока и обсудите с учеником, какие из них удалось достичь.

Примеры итогов, которые может озвучить школьник:

• научился связывать углы и стороны в прямоугольном треугольнике;
• изучил синусы, косинусы, тангенсы и котангенсы;
• сформулировал тригонометрические тождества;
• решил n задач;
• доказали n формул;
• закрепил знания по теореме Пифагора и подобным треугольникам.

Домашнее задание

Задание 1. Найти тригонометрические функции острых углов в треугольнике со сторонами 9, 40, 41. 

Задание 2. 

Задание 3.

Найти АВ, если известно, что в прямоугольном треугольнике АВС угол В = 90°, АС = 28, sin угла С равен ⁴⁄₇

Задание 4.

Задание 5. В прямоугольном треугольнике острые углы А и В. Известно, что sin угла А равен ⁵⁄₁₃

Нужно найти остальные значения.

Надеюсь, что план урока по теме «Основное тригонометрическое тождество» поможет сэкономить преподавателям время и силы, а ученикам преодолеть еще один барьер к успешной сдаче ОГЭ. Какие еще темы тяжело даются вашим ученикам, напишите в комментариях!