Разбор 8 задания из ОГЭ по информатике

Главное, что должны понять ваши ученики, прежде чем начнут решать задачи на логику:

Подробно разберем в этой статье все, что пригодится для успешного решения 8 задания ОГЭ по информатике.

Содержание:

1. Какие цели и задачи у этой статьи
2. Что такое логические задачи в информатике
3. Как выглядит логическая структура сложного высказывания
4. Основные операции алгебры логики
5. Необязательные в школьной программе операции
6. Как записывать и читать логические выражения
7. Как запомнить порядок выполнения логических операций
8. Пирамида приоритетов
9. Что такое логические множества
10. Что такое круги Эйлера
11. Графическое изображение логических множеств с помощью кругов Эйлера
12. Задачи на поиск в Сети и диаграммы Эйлера

1. Какие цели и задачи у этой статьи

Цели:

• Познакомиться с основными понятиями математической логики и теории множеств.
• Изучить принципы поиска информации в интернете и других хранилищах информации.
• Научиться вычислять количество получаемой в результате запросов для поисковых серверов информации с использованием логических выражений.

Задачи:

• Познакомиться с основными понятиями алгебры логики.
• Повторить определения основных логических операций и их приоритеты.
• Повторить основные операции над множествами и установить аналогию между логическими операциями и операциями над множествами.
• Научиться решать задачи на поиск в Сети с помощью диаграмм Эйлера.

2. Что такое логические задачи в информатике

Информатика основана на логике. Логика оперирует высказываниями и их взаимодействиями. 

Высказывание — это предложение с любым утвердительным содержанием, которое может быть либо истинным, либо ложным. На языке информатики истинностное значение — это 1 или true, а ложное — это 0 или false.

3. Как выглядит логическая структура сложного высказывания

Логическое рассуждение = простое высказывание + «НЕ», «И», «ИЛИ», «ЕСЛИ… ТО», «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» и другие частицы и словоформы → сложное высказывание.

Словоформы и частицы — это логические операции, связывающие высказывания. 

Операции выполняются над высказываниями и позволяют сделать вывод об истинности или ложности сложного высказывания по истинности и ложности составляющих его элементарных высказываний.

Еще полезные материалы:

4. Основные операции алгебры логики

1. «НЕ», отрицание, ¬А

Отрицание высказывания А — это высказывание, истинное тогда и только тогда, когда высказывание А ложно.

2. «И», конъюнкция, А ∧ В
   Конъюнкция высказываний А и В — это высказывание, истинное тогда и только тогда, когда истинны оба высказывания.

3. «ИЛИ», дизъюнкция, А ∨ В
   Дизъюнкция высказываний А и В — это высказывание, ложное тогда и только тогда, когда оба высказывания ложны.
   
4. «ЕСЛИ… ТО», импликация, А → В
   Импликация высказываний А и В — это высказывание, ложное тогда и только тогда, когда А истинно, а В ложно.

5. «ТОГДА И ТОЛЬКО ТОГДА, КОГДА», эквиваленция, А ↔ В
   Эквиваленция высказываний А и В — это высказывание, истинное тогда и только тогда, когда значения А и В совпадают.

5. Необязательные в школьной программе операции

6. Как записывать и читать логические выражения

1. Без скобок — так будет проще.
2. По правилу приоритетов: сначала выполняются самые «сильные» операции, затем — более «слабые».

7. Как запомнить порядок выполнения логических операций

Порядок выполнения логических операций: «НЕ», «И», «ИЛИ», импликация.

Или «Если мама сказала: „НЕ“, то так и будет! Если мама сказала: „Сделай это И это“, то сначала сделай это И это, а уже потом думай свое „ИЛИ“. Все выводы (импликация) — после».

8. Пирамида приоритетов

Для тех, кто хочет связать свою жизнь с программированием и информатикой.

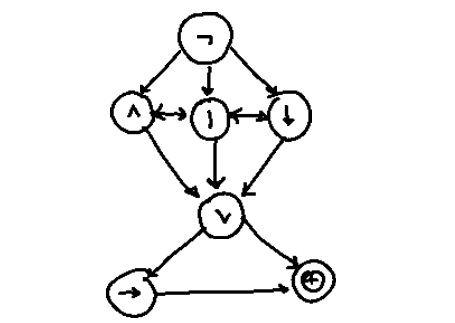
Указаны все логические операции, включая штрих Шеффера, стрелку Пирса и сложение по модулю 2.

9. Что такое логические множества

Множество — это любая совокупность определенных и различимых между собой объектов окружающей действительности или нашего воображения, объединенная по какому-либо признаку. Эти объекты называются элементами множества. Множества обозначаются большими буквами латинского, русского или любого другого алфавита.

В математике понятие множества принадлежит к числу первичных, то есть не определяемых через более простые.

10. Что такое круги Эйлера

Круги Эйлера — наглядная геометрическая модель для объяснения отношений между подмножествами.

В определении множества нет никаких ограничений по природе элементов. Это может быть множество учеников восьмого класса, множество белок в лесу, множество звезд на небе и так далее. В качестве элементов множеств могут быть также множества. 

В математике часто используют числовые множества, элементами которых являются числа. Из школьной алгебры известны числовые множества:

• N — натуральные;
• Z — целые;
• Q — рациональные;
• I — иррациональные;
• R — действительные.

Если множество содержит конечное число элементов, то оно называется конечным, а в противном случае — бесконечным. 

Подмножеством A множества B (A ⊆ B, или A содержится в B) называется множество A, каждый элемент которого принадлежит B. 

Легче всего запомнить теорию, если она наглядная.

11. Графическое изображение логических множеств с помощью кругов Эйлера

В основе теории множеств лежат первичные понятия: множество и его отношения с элементами множества (обозначается как «X есть элемент множества A»).

Определены следующие операции над множествами:

• Объединение, сумма, A ∪ B
  

Объединение — это множество всех элементов, принадлежащих A или B. 

• Пересечение, произведение, A ∩ B
  

Пересечение множеств С = A ∩ B — это множество элементов, принадлежащих A и B.

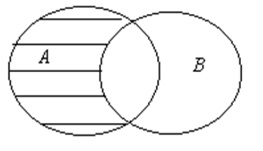
• Разность, A \ B

Разность A \ B — это множество, состоящее из элементов A, не входящих во множество В.

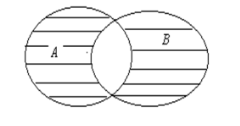
• Симметрическая разность, A △ B
  Симметрическая разность A △ B — это множества непересекающихся элементов A и В.

Для множеств определены следующие бинарные отношения:

• равенства (A = B);
• включения (A ⊂ B).

12. Задачи на поиск в Сети и диаграммы Эйлера

Задача 1

После урока биологии несколько учеников отправили запросы в школьную базу знаний. Они хотели увидеть изображения животных, которых не было в учебнике. 

В списке ниже приведены эти запросы. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для обозначения логической операции «И» — символ &.

1. Сервалы & манулы & ирбисы
2. Сервалы & ирбисы
3. Сервалы | ирбисы
4. Сервалы | манулы | ирбисы

Расположите номера запросов в порядке убывания количества изображений, которые нашел SQL-сервер по каждому запросу. 

Решение

Запишите запросы как математические выражения со знаками + и ⋅:

X₁ = A ⋅ B ⋅ C.
X₂ = A ⋅ B.
X₃ = A + B.
X₄ = A + B + C.

Изобразите диаграммы с областями:

Сравните нарисованные диаграммы. Найдите последовательность областей в порядке уменьшения. 

Важно: каждая следующая область включает в себя предыдущую.

Ответ: 4321.

Задача 2

Домен крупной компании — производителя бытовой техники состоит из 1000 сайтов интернет-магазинов по всему миру. У администраторов домена есть обновляемая каждый день таблица ключевых слов для сайтов этого домена. Вот ее фрагмент:

Ключевое слово	Количество сайтов, для которых это слово является ключевым
сушилка	200
паровой утюг	250
микроволновка	450

Сколько сайтов будет найдено по запросу «(паровой утюг | сушилка) & микроволновка», если по запросу «паровой утюг | сушилка» было найдено 450 сайтов, по запросу «паровой утюг & микроволновка» — 40, а по запросу «сушилка & микроволновка» — 50?

Решение

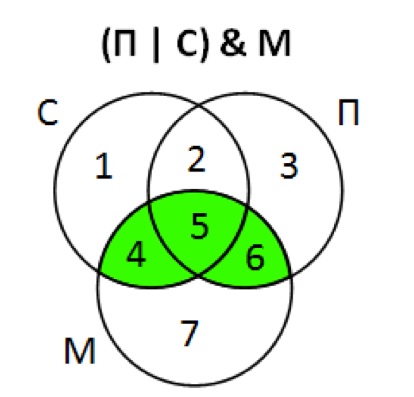
Обозначьте ключевые слова буквами C, П, М и нарисуйте эти области в виде кругов Эйлера.

Запрос «(П | C) & M» в точности соответствует объединению областей 4, 5 и 6 на рисунке.

Количество сайтов, удовлетворяющих запросу в зеленой области, будем обозначать через N_i.

Уравнения, которые определяют запросы:

сушилка	N1 + N2 + N4 + N5 = 200
паровой утюг	N2 + N3 + N5 + N6 = 250
паровой утюг | сушилка	N1 + N2 + N4 + N5 + N3 + N6 = 450

Из первого и третьего уравнений сразу следует: 200 + N₃ + N₆ = 450 ⇒ N₃ + N₆ = 250.
Из второго уравнения: N₂ + N₅ + 250 = 250 ⇒ N₂ + N₅ = 0.
Поскольку количество сайтов не может быть отрицательной величиной, N₂ = N₅ = 0.
Учитываем, что N₅ = 0.

«Паровой утюг & микроволновка»: N₅ + N₆ = 40 ⇒ N₆ = 40.
«Сушилка & микроволновка»: N₄ + N₅ = 50 ⇒ N₄ = 50.

Таким образом, «(паровой утюг | сушилка) & микроволновка»: N₄ + N₅ + N₆ = N₄ + N₆ = 40 + 50 = 90.

Ответ: 90.

Задача 3

По заказу администрации спортивной школы была собрана информация о количестве запросов, сделанных детьми в возрасте шестнадцати лет. Они выбирали себе спортивную специализацию: бокс или самбо. 

Ниже приведены результаты, которые выдал поисковый сервер по их запросам в интернете:

бокс | самбо	7770
самбо	5500
бокс & самбо	1000

Сколько страниц будет найдено по запросу «бокс»?

Решение

Первый способ

Х = 7770 − 5500 = 2270.
Бокс = Х + 1000 = 2270 + 1000 = 3270.

Второй способ

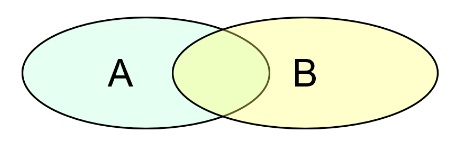
N_A + N_B = N_A & N_B + N_A | N_B.
N_B = N_A & N_B + N_A | N_B − N_A.
N_A = 1000 + 7770 − 5500 = 3270.

Ответ: 3270.

Задача 4

Ниже приведена таблица, в которой указаны запросы и количество страниц, выданных поисковым сервером. Все запросы были сделаны студентами-химиками за прошедшую неделю в научно-популярном блоге.

лантан & (радий | щелочь)	320
лантан & радий	200
лантан & радий & щелочь	50

Сколько страниц будет найдено по запросу «лантан & щелочь»?

Решение

b + a = 200 a + b + d = 320 a = 50 Найти: a + d

b = 200 − 50 = 150.
a + d = 320 − b = 320 − 150 = 170.

Ответ: 170.