Формулы сокращенного умножения: методика и задания
Школьники часто клеймят алгебру сложным и непонятным предметом после темы «Формулы сокращенного умножения» (ФСУ). Однако с их помощью можно быстро преобразовать выражения и устно считать.
В этой статье делимся методикой и упражнениями, которые помогут вашим ученикам понять, запомнить и полюбить ФСУ. Рассмотрим тему на примере формул квадрата суммы и квадрата разности.
Содержание:
- Темы-предшественники ФСУ
- Начало изучения темы ФСУ
- Формулы сокращенного умножения
- Связь с геометрией
- Упражнения
- Варианты формул
- Упражнения
- Устный счет с помощью ФСУ
Учите школьников и получайте
от 40 до 100 000 рублей в месяц!
Приглашаем учителей математики
с высшим образованием (или студентов последнего курса) и опытом подготовки
к выпускным экзаменам
Темы-предшественники ФСУ
Чтобы школьник понял, откуда взялась тема «Формулы сокращенного умножения», ее нужно подать как следствие умножения многочленов. Убедитесь, что у вашего ученика нет проблем с умножением двучленов.
(6d + 3)(2 + 8d)
(2x + 7)(3 – 5x)
(3a2 – b3)(a3 – 4b2)
Поставленная математическая речь — преимущество в изучении ФСУ. Потренируйтесь с учащимся правильно озвучивать выражения.
a + b * c
сумма числа а и произведение чисел b и c
d2 – f : e
разность квадрата d и частного чисел f и e
(а * b + c2)2
квадрат суммы произведения чисел a и b и квадрата c
Сколько платят в Skyeng преподавателю математики?
Из чего складывается доход учителей, рассказываем в специальной статье.
Подробне
Начало изучения темы ФСУ
Предложите ребенку выполнить однотипные вычисления (примеры). Так вы сформируете фундамент для понимания новой темы. Попросите ученика раскрыть скобки в примерах и найти закономерность.
(2 + c)(2 + c)
(6a + 4)(6a + 4)
(a2 + b)(a2 + b)
Школьник поймет: вместо того, чтобы каждый раз раскрывать скобки, можно использовать формулы.
Формулы сокращенного умножения
Покажите ученику общие случаи квадрата суммы и квадрата разности. Попросите доказать их через правила умножения двучленов.
(a + b)2= a2 + 2ab + b2
Формула квадрата разности
(a − b)2= a2 − 2ab + b2
Дайте названия формулам и пользуйтесь ими на уроках. Избегайте зачитывания, например, «а плюс b в квадрате», и закрепляйте математическую речь.
Связь с геометрией
Дети приходят в восторг, когда сухие буквы и числа обретают материальное объяснение. Приведите геометрические доказательства формул. Это покажет связь между алгеброй и геометрией и закрепит понимание справедливости ФСУ.
Геометрическое доказательство квадрата суммы
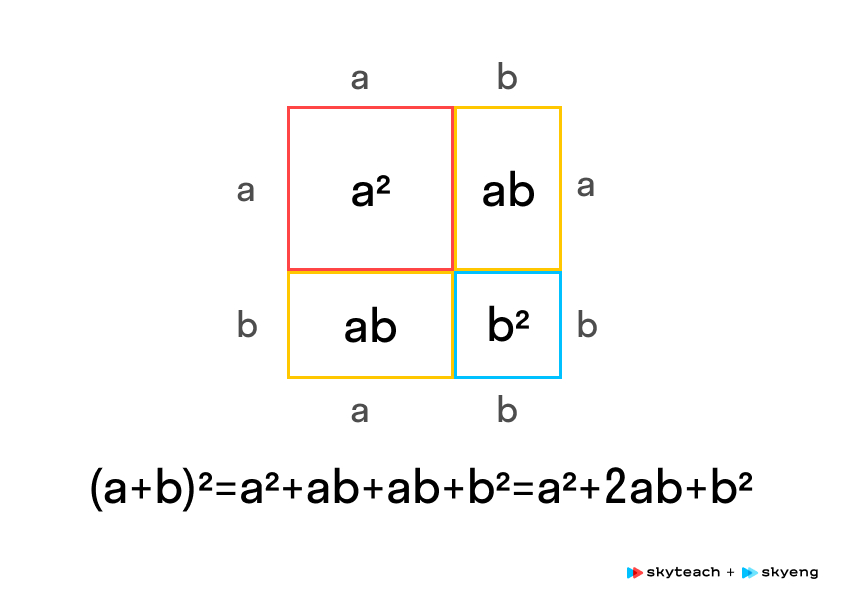
Геометрическое доказательство квадрата разности
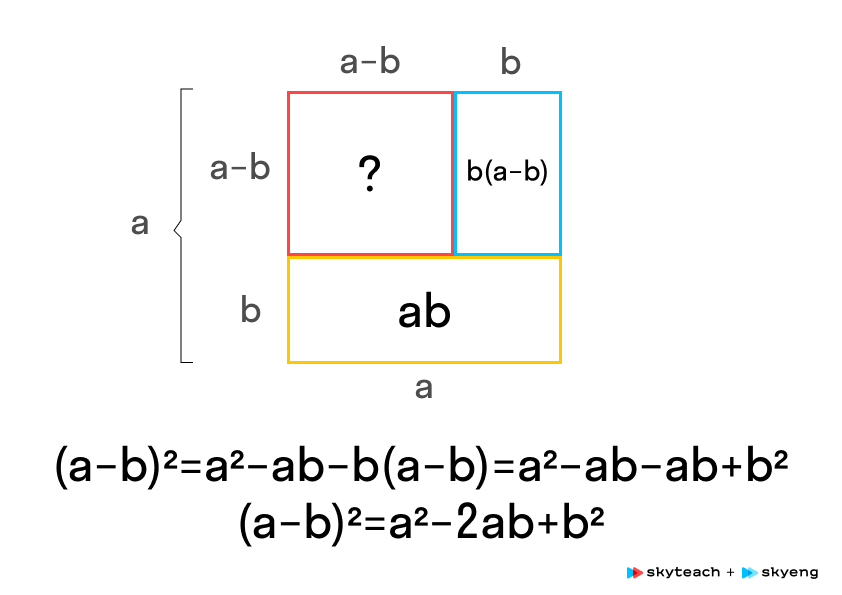
Упражнения
Для закрепления формул сокращенного умножения дайте ученику много однотипных примеров. Если школьник не понимает, как работают ФСУ, предложите выполнить вычисления вручную — без формулы. Так на контрольных и экзаменах ребенок не растеряется, если забудет формулы.
(7к − 8m)2
(1,2x − 0,5у)2
(3x2 + 7y3)2
(4ab2 − a2b)2
(3⁄4d + 1⁄2e)2
Включите в занятия упражнения на обратный переход от многочлена к произведению двучленов.
х2 + 49 + 14х
25х2 − 80ху + 64y2
Варианты формул
Рассмотрите с учеником ситуации, похожие на классические квадрат суммы и квадрат разности.
(−а + b)2 = a2 − 2ab + b2 = (a − b)2 = (b − a)2
(−а − b)2 = a2 + 2ab + b2 = (a + b)2
Не давайте эти формулы на заучивание. Цель — увидеть сходства с классическими формулами и отработать навыки вычислений в нестандартных примерах.
Упражнения
Закрепить понимание формул помогают упражнения на заполнение пропусков.
(b + *)2 = * + * + 4c4
(* + *)2 = * + 70b3с + 49с2
Устный счет с помощью ФСУ
Вишенка на торте — применение формул для устного счета. Благодаря им можно легко возводить в квадрат двузначные числа.
422 = (40 + 2)2 = 1600 + 160 + 4 = 1764
592 = (60 − 1)2 = 3600 − 120 + 1 = 3481
682 = (70 − 2)2 = 4900 − 280 + 4 = 4624
С помощью ФСУ выводится и правило возведения в квадрат чисел, которые оканчиваются на 5.
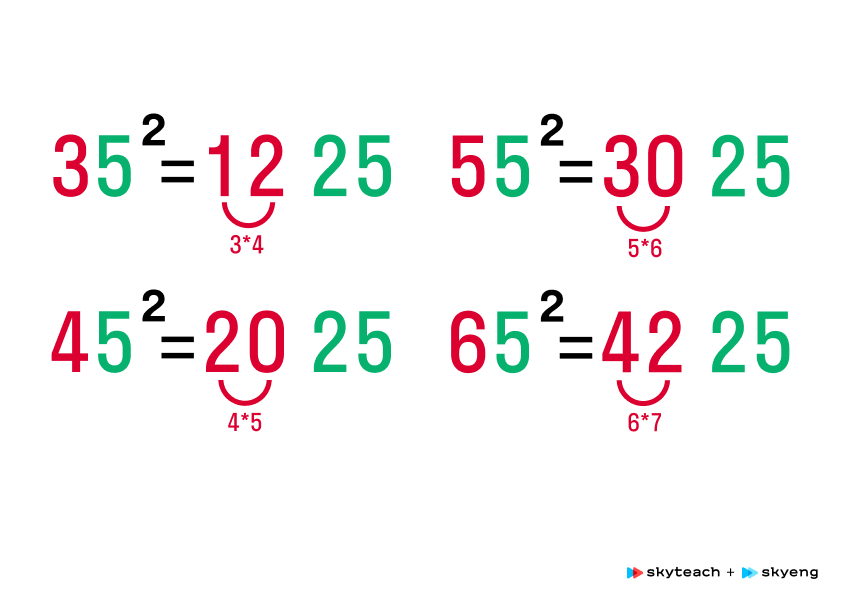
Ирина Чегринская 
Анна Михайлова-Левина 