Понятие числа возникло из-за практической необходимости подсчета предметов. Сначала предметы считали при помощи подручных средств: пальцев, камней, еловых шишек и т. д. На ранних стадиях развития человечества запас чисел был весьма ограничен. Ряд известных и используемых натуральных чисел был конечен и удлинялся не очень быстро. Осознание же неограниченной продолжительности натурального ряда чисел стало уже признаком достаточно высокого уровня знаний и культуры.
Вместе с использованием увеличивающихся чисел развивались и сами символы, которыми обозначались числа, а сами числа образовывали системы.
Развитие человечества постепенно приводило и к совершенствованию систем счисления. Употребляемая сейчас позиционная десятичная система счисления является итогом длительного исторического развития.
- Вопрос 1: кто придумал 0?
- Вопрос 2: единица — это простое число или составное?
- Вопрос 3: сколько множеств чисел проходят в школе?
- Вопрос 4: где находится основание и что такое показатель?
- Вопрос 5: может ли когда-нибудь случиться так, что иррациональное число станет рациональным или наоборот?
- Вопрос на миллион (дополнительно для продвинутых): как называются числа, которые можно нарисовать в виде вектора?
План урока:
1. Действительные числа
- Положительные числа — числа, которые больше нуля.
- Отрицательные числа — числа, которые меньше нуля.
- 0 (ноль) — число, находящееся между положительными и отрицательными числами (это число придумал индийский математик Брахмагупта).
- Натуральные числа — числа, появившиеся при счете: 1, 2, 3, 4 и т. д.
- Целые числа — числа, которые состоят из натуральных чисел, нуля и чисел, противоположных натуральным: …, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, …
- Простые числа — числа, которые имеют ровно два делителя, то есть 1 и само число.
- Составные числа — числа, которые имеют более двух делителей, то есть, помимо деления на 1 и на само число, составное число также можно разделить как минимум на одно положительное целое число.
- 1 не является простым или составным числом.
- Рациональные числа — числа, которые могут быть представлены в виде дроби p/q, где числа p и q целые, отличные от нуля.
Кроме этого, дробь p/q может быть также представлена:
— либо как конечное десятичное число: 7/4=1,75;
— либо как повторяющееся десятичное число: 7/3=2,333333333…
- Иррациональные числа — числа, которые невозможно представить в виде рациональной дроби p/q.
Иррациональное число не может быть представлено в виде дроби p/q с целыми p и q.
Типичные примеры иррациональных чисел:
π=3,14592652589793…
e=2,718281828459045…
√3=1,73205080756887…
Иррациональные числа не могут быть рациональными и наоборот!
Есть еще одна очень важная классификация чисел:
- Четные числа — числа, которые при делении на 2 дают в остатке 0.
- Нечетные числа — числа, которые при делении на 2 не дают в остатке 0.
Примеры:
- Каким числом является число 5? (За полный ответ полагается соответствующая оценка.)
Ответ: положительное, натуральное, целое, рациональное, действительное.
- Каким числом является число −4,2?
Ответ: отрицательное, рациональное, действительное.
- Каким числом является число 666/13?
Ответ: положительное, иррациональное, действительное.
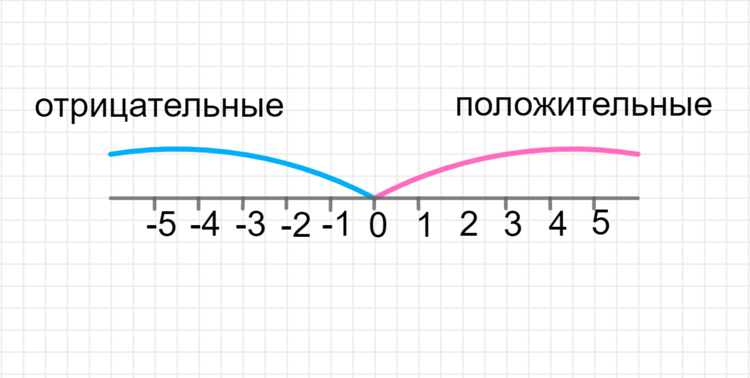
Существует однозначное соответствие между набором действительных чисел и точками на прямой с действительными числами: каждая точка на этой прямой соответствует действительному числу и наоборот. Все положительные действительные числа представлены точками, лежащими справа от числа ноль, а все отрицательные действительные числа представлены точками слева от числа ноль. Все положительные числа расположены в порядке возрастания слева направо — справа от нуля; все отрицательные целые числа расположены в порядке убывания справа налево — слева от нуля.
Большинство алгебраических манипуляций основано на свойствах действительных чисел. Все действительные числа обладают следующими свойствами:
- Свойство симметричности: «Равенство a=b подразумевает равенство b=a».
Пример: равенство x+y=z подразумевает равенство z=x+y.
- Свойство транзитивности (переходное свойство): «Два числа равны друг другу, если каждое из них равно одному и тому же числу».
Другими словами: «Уравнения a=b и c=b подразумевают, что a=c».
Пример: уравнения x+y=z и z=b+c подразумевают, что x+y=b+c.
- Свойство замены: «Любое число может быть заменено на равное ему в любом выражении».
Если a=b, то a может быть заменено на b в любом математическом выражении.
Пример: если x=a и x+b=c, то a+b=c.
- Свойство сложения и вычитания: «Если к равным числам прибавляются равные числа, то суммы равны. Если из равных чисел вычесть равные числа, то разности равны».
Пример: если a=b и c=d, то a ± c=b ± d.
- Свойство умножения: «Если равные числа умножаются на равные числа, то произведения равны».
Пример: если a=b и c=d, то ac=bd.
Числа в произведениях называются сомножителями.
- Коммутативные законы сложения и умножения: «Числа могут складываться в любом порядке: a+b=b+a. Числа могут умножаться в любом порядке: ab=ba».
- Ассоциативные законы сложения и умножения: «Слагаемые могут сочетаться в любые группы: a+(b+c)=(a+b)+c. Сомножители могут сочетаться в любые группы: a(bc)=(ab)c».
- Дистрибутивный закон: «Скобки можно раскрыть; общий множитель можно вынести за скобки».
a(b ± c)=ab ± ac
(a ± b)c=ac ± bc
- Аксиома тождества для суммы: «Сумма любого действительного числа и числа 0 есть само это число: a+0=a».
- Аксиома тождества для произведения: «Произведение любого действительного числа и числа 1 есть само это число: a×1=a».
- Аксиома инверсии для сложения: «Для любого действительного числа a существует уникальное число (-a), такое, что a+(-a)= -a+a=0. Число (-a) называется противоположным числу a».
Можно сказать, что вычитание — это действие, обратное сложению, а сложение — это действие, обратное вычитанию.
Сложение и вычитание являются операциями, обратными друг другу.
- Аксиома инверсии для произведения: «Для любого ненулевого числа a существует уникальное действительное число (1/a), такое, что a×(1/a)=(1/a)×a=1. Число (1/a) называется обратным числу a».
Умножение и деление являются операциями, обратными друг другу.
- Для любых действительных чисел a и b истинным может быть только одно соотношение: a>b, a=b, a<b .
2. Модуль и свойства модуля
Определение. Модуль действительного числа a записывается так: |a|. А определяется так: |a|={a, если a ≥ 0; -a, если a<0}.
Примеры: |5|=5; |-5|=5; |0|=0.
Полезное наблюдение: для любых чисел a и b расстояние между a и b на числовой прямой есть модуль разности этих чисел |a-b|=|b-a|.
Пример: |-5|=5, так как число -5 располагается на числовой прямой на таком же расстоянии от числа 0, что и число 5.
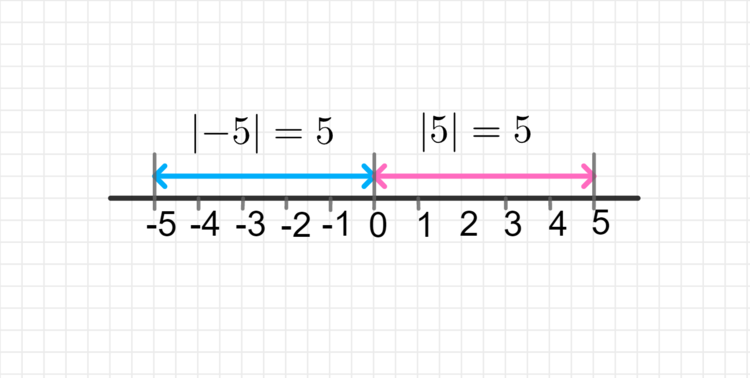
Свойства:
- |a| ≥ 0.
- |a|=0 тогда и только тогда, когда a=0.
- |a×b|=|a|×|b|.
- |a/b|=|a|/|b|, если b ≠ 0.
- |−a|=a.
- |a−b|=|b-a|.
- |a|2=a2.
3. Дроби
Дробью называется число, записанное в виде a\b, где a называется делимым, а b — делителем. Оба числа, делимое и делитель, являются действительными числами, но делитель не должен быть равен нулю.
Дроби имеют следующие свойства:
- Дроби сохраняют свое значение, когда делимое и делитель одновременно умножаются или сокращаются на одно и то же ненулевое число: ac/bc=a/b.
Примеры:
- 45/60=5×3×3/5×3×2×2=3/4.
- x2-5x+6/x−3=(x−2)(x−3)/(x−3)=(x−2).
- Чтобы складывать (или вычитать) дроби с одинаковыми знаменателями, объединяйте числители и оставляйте тот же знаменатель: a/b+c/b=a+c/b или a/b-c/b=a−c/ b.
- Чтобы сложить (или вычесть) дроби с разными знаменателями, приведите дроби к общему знаменателю, найдя общий множитель обоих знаменателей, а затем сложите (или вычтите) получившиеся дроби с одинаковыми знаменателями: a/b±c/d=ad/bd±bc/bd=ad±bc/bd.
Примеры:
- 5/7-3/13=5 × 13/7 × 13-3 × 7/13 × 7=65 − 21/91=44/91.
- 1/ab+1/bc=c/abc+a/abc=a + c/abc.
• Числитель произведения дробей равен произведению числителей, а знаменатель равен произведению знаменателей всех дробей: a/b×c/d=ac/bd.
Чтобы разделить две дроби, переверните вторую дробь и выполните умножение двух дробей: 
Пример: 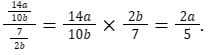
- Пропорции могут быть решены путем перекрестного умножения с использованием свойства перекрестного умножения: «Из a/b=c/d также следует, что d/b=c/a или a/c=b/d».
Пример: если x/y=z/w, то x/y=2x — 7z/2y — 7w=3x + 15z/3y + 15w.
• Какие направления по математике есть в Skyeng?
• Как стать преподавателем математики в Skyeng?
4. Множества
Множество — это конечный набор объектов. Объекты называются элементами или членами множества. В качестве имен множеств используют заглавные буквы.
Если множество A определяется списком своих элементов, то его можно записать в следующем формате:
A={список элементов}
- Если элемент x является элементом множества A, то это записывается как x ∈ A.
- Если элемент x НЕ является элементом множества A, то это записывается как x ∉ A.
Множество A можно также определить, описывая его элементы через характеризующие их свойства: «Множество A всех элементов x, таких, что x обладает свойством P». В этом случае символ | используется вместо утверждения «такой, что», а множество записывается в следующем формате:
A={ x | P}
Самые важные множества:
- Множество натуральных чисел: N={1, 2, 3, 4, 5,…. }
- Множество целых чисел: I={-3, -2, -1, 0, 1, 2, 3, …. }…,
- Множество рациональных чисел: Q={p/q | q ≠ 0; p,q ∈ I}.
- Множество иррациональных чисел: H.
- Множество действительных чисел. R
Сравнение множеств:
- Множество A равно множеству B, если каждый элемент A является элементом B, и наоборот: A=B.
Пример: {b, a, c}={c, a, b}.
- Множество A называется собственным подмножеством множества B, если каждый элемент множества A является элементом B, но A ≠ B: A ⊂ B.
Примеры:
- Множество натуральных чисел является собственным подмножеством множества действительных чисел: N⊂R.
- Множество {a, b, c} является собственным подмножеством множества {a, b, c, d}: {a, b, c }⊂{a, b, c, d}.
- Множество A называется подмножеством множества B, если A является правильным подмножеством B либо A=B: A ⊆ B.
Пример: {a, b, c }⊆{ a, b, c}.
- Пересечение множеств A и B — это множество всех элементов, которые находятся как в A, так и в B: A ∩ B.
Пример: если A={a, b, c } и B={a, c, d, e, f }, тогда A ∩ B={a, c }.
- Объединение множеств A и B — это множество всех элементов, которые находятся либо в A, либо в B, либо в обоих: A ∪ B.
Пример: R=HQ.
5. Интервалы
Интервалы — это специальные подмножества действительных чисел.
Интервал может быть конечным или бесконечным. Конечный интервал действительных чисел лежит между двумя действительными точками, a и b. Бесконечный интервал имеет только одну конечную точку и содержит все остальные действительные числа, лежащие в направлении положительной или отрицательной бесконечности от этой точки.
- Если набор действительных чисел лежит между a и b, но не включает ни одно из них, интервал является открытым.
- Если обе конечные точки, a и b, включены в набор, интервал называется замкнутым.
- Полуоткрытый интервал содержит либо a, либо b.
- Бесконечный интервал не ограничен ни вправо, ни влево, и символ бесконечности всегда заключен в круглую скобку, как у открытого интервала. В то же время бесконечный интервал может быть открытым или закрытым в конечной точке.
Таким образом, мы имеем следующие случаи:
- интервал полубесконечный слева: (-∞; b]
- интервал полубесконечный справа: [a; +∞)
- бесконечный интервал : (-∞;+∞)
- конечный интервал: [a; b]
6. Степени
В выражении xa величина x называется основанием, а величина a — показателем степени.
Следующие математические правила полезны при алгебраических операциях со степенями:
- Любое ненулевое действительное число, возведенное в нулевую степень, равно единице: x0=1(x ≠ 0).
- Ненулевое действительное число, возведенное в степень (-a), является обратной величиной того же действительного числа, возведенного в степень a: x-a=1/xa (x ≠ 0).
Чтобы умножить степени с одинаковыми основаниями, сложите их показатели: xa × xb=xa + b.
- Чтобы разделить степени с одинаковыми основаниями, вычтите из показателя степени числителя показатель степени знаменателя: xa/xb=xa − b (x ≠ 0).
- Чтобы возвести в степень выражение, которое стоит в другой степени, перемножьте показатели степени: (xa)b=xab.
- Произведение двух величин, возведенное в степень, равно произведению каждой из этих величин, возведенных в степень: (xy)a=xaya.
Дробь, возведенная в степень, равна дроби, в числителе и знаменателе которой находятся возведенные в ту же степень числитель и знаменатель исходной дроби: (x/y)a=xa/ya (y ≠ 0).
7. Рациональные степени
Примечание: у всех корней n-ной степени индекс n является натуральным числом, бóльшим единицы: n ∈ N, n>1.
Говорят, что число y является корнем n-ной степени действительного числа x, если yn=x.
Корень n-ной степени числа x обозначается как n√x или x1/n.
Таким образом, связь между степенью и корнем записывается так: n√x=x1/n.
Наиболее важные правила для степеней рациональных чисел:
- x0=1.
- x-a=1/xa, x ≠ 0.
- xa × xb=xa + b.
- xa/xb=xa — b, x ≠ 0.
- (xa)b=xab.
- (xy)a=xaya.
- (x/y)a=xa/ya, y ≠ 0.
- n√x=x1/n.
- √x2=|x|.
- n√xm=xm/n.
- n√xy=n√x × n√y.
- n√x/y=n√x/n√y, y ≠ 0.



















 Ирина Чегринская
Ирина Чегринская