Физика ЕГЭ 26 задание

В 2024 году структура экзамена по физике была переработана и изменена. В результате этого задание 26 стало последним. Оно имеет высокий уровень сложности, для которого необходимо уметь решать расчетные задачи с неявно заданной физической моделью с использованием различных законов и формул из раздела «Механика», обосновывая выбор физической модели для решения задачи. Задание 26 относится к части 2, где необходимо написать развернутый ответ на задание. Оценивается в 4 балла.

Чтобы получить 4 балла, необходимо помнить о том, что каждая задача с развернутым ответом проверяется экспертом, который следует критериям. То есть необходимо оформить это все таким образом, чтобы у экспертов не было никаких претензий к вашему решению. Поэтому давайте рассмотрим эти правила на примере решения задачи.

Разбор примера задания 26 ЕГЭ по физике

Итак, давайте пройдемся по критериям, которые влияют на итоговый балл.

1. После того как вы правильно записали «Дано», по необходимости перевели все единицы измерения в системные, необходимо сделать чертеж (рисунок), на котором верно и адекватно указаны направления векторов.

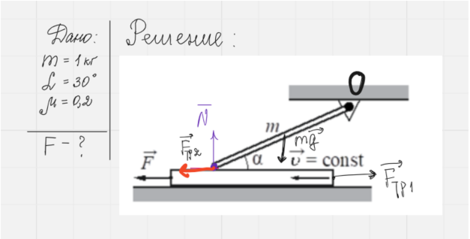
2. Описать все вновь вводимые величины. Например, если в условии не было ничего сказано о длине стержня, а вы используете его при решении, то вы обязательно должны вынести его на рисунок или указать, что:

l — это длина стержня;
F_тр1 (F_тр2) — сила трения со стороны доски на стержень (сила трения со стороны стержня на доску);
N — сила реакции опоры;
М_{1, 2, 3} — моменты сил тяжести, трения, силы реакции опоры.

3. Записать положения теории и физические законы, закономерности, необходимые для решения задачи. Например, при решении данной задачи — второй и третий законы Ньютона, выражение для силы трения скольжения, условие равновесия твердого тела через момент сил.

В ИСО доска движется равномерно и прямолинейно, поэтому равнодействующая его сил равна нулю, то есть + _тр1 = 0. Проекция векторов силы на ось Ох: F — F_тр1 = 0; F = F_тр1.

Согласно третьему закону Ньютона: _тр1 = —_тр2 , поэтому F = F_тр2.

Условие равновесия (правило моментов), относительно точки О:  M1 + M2 + M3 = 0.

4. Необходимо привести все математические преобразования поэтапно. Не стоит пропускать несколько математических действий, вычисляя их в уме. Решение должно быть плавным и развернутым, приводящим к правильному числовому ответу, при этом допускается решение «по частям» с промежуточными вычислениями.

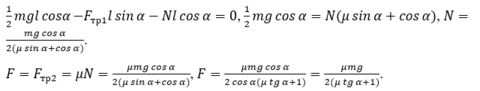
5. В ответе должен быть получен правильный численный ответ с указанием размерности и подставленными величинами.

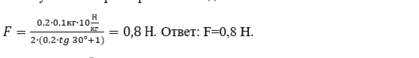
6. Верно обосновать возможность использования законов (закономерностей), их применимость использования для конкретно заданной задачи. Не имеет значения, где написано обоснование: в начале или конце задачи. Главное, указать, что при решении мы всегда работаем в условиях некоторой модели (например, ИСО, модель материальной точки и т. д.). Обратите внимание на то, что не стоит объединять в одном предложении более двух утверждений. 

Вам могут быть интересны и эти материалы к подготовке к ЕГЭ по физике:

Обоснование:

1. Систему отсчета свяжем с Землей. Будем считать эту систему отсчета инерциальной (ИСО).
2. Будем считать доску материальной точкой, так как она движется поступательно.
3. Движение доски в ИСО можно описать с помощью законов Ньютона, сформулированных для материальных точек.
4. Согласно третьему закону Ньютона, силы, с которыми доска и стержень взаимодействуют друг с другом, равны по модулю и противоположны по направлению.
5. Опишем стержень моделью твердого тела, так как форма и размеры тела неизменны, как и расстояние между любыми двумя точками тела.
6. Так как по условию задачи стержень находится в состоянии покоя относительно поступательного движения доски, то сумма приложенных внешних сил к стержню равна нулю. 
7. Сумма моментов этих сил относительно оси, проходящей перпендикулярно плоскости рисунка через точку О (шарнирное крепление), равна нулю, так как стержень в покое. 

Таким образом, при невыполнении одного из указанных критериев будут сниматься баллы. Особое внимание стоит уделять последнему пункту критериев, хоть за него и дают всего один балл, очень вероятно, что именно этот балл может стать решающим. Что же следует указать в обосновании? Давайте разберем более подробно.

Первый, второй, третий законы Ньютона, а также законы сохранения импульса и энергии применимы в рамках инерциальной системы отсчета (ИСО). Планета Земля не является идеальной ИСО, так как она вращается одновременно вокруг своей оси и вокруг Солнца, следовательно, и все тела на ее поверхности движутся неравномерно. Но возникающие эффекты такого движения крайне малы, и зачастую ими пренебрегают. Поэтому обязательными пунктами в обосновании применимости данных законов станут:

1. Инерциальная система отсчета.
2. Материальная точка.
3. Законы Ньютона.
4. Абсолютно твердое тело.
5. Нить. Блоки. Пружины.
6. Сила трения.
7. Закон сохранения энергии (ЗСЭ).
8. Закон сохранения импульса (ЗСИ).

1. Инерциальная система отсчета.

Примеры: 

• Перейдем в систему отсчета, связанную с Землей. Будем считать ее инерциальной.
• Рассмотрим задачу в системе отсчета, связанной с Землей. Будем считать ее инерциальной.
• Задачу будем решать в инерциальной системе отсчета, связанной с поверхностью Земли.
• Систему отсчета, связанную с Землей, будем считать инерциальной.

Однако бывают случаи, когда ИСО связывают не с Землей, а с другим покоящимся телом. Например, в данной задаче инерциальную систему отсчета можно связать со столом.

• Задачу будем решать в инерциальной системе отсчета, связанной с поверхностью стола.

Так или иначе, важно, чтобы система отсчета оказалась инерциальной.

2. Материальная точка.

Модель материальной точки имеет большое значение в механике. Вводится для упрощения решения задач, так как если размерами груза не пренебрегать, то придется учитывать множество иных факторов, таких как вращение тела вокруг своей оси. А при записи закона сохранения энергии учитывать и энергию вращения тела, что зачастую усложняет задачу, но не оказывает существенного влияния на итоговый результат. Поэтому вводим модель материальной точки и обязательно обосновываем ответ.

Размер тела намного меньше по сравнению с другими телами в задаче (длина нити, пружины, горки, пройденного пути и т. д.):

• Будем считать тело материальной точкой, так как тело мало в сравнении с радиусом «мертвой петли».
• Шарики имеют размеры намного меньше по сравнению с длиной нити маятника, поэтому описываем их моделью материальной точки.

Если тело (система тел) движется поступательно:

• Тела движутся поступательно, их можно рассматривать как материальные точки (смотреть рис. 2).
• Тело описывается моделью материальной точки, так как двигается поступательно.

Возможно, вас заинтересуют статьи о преподавании в онлайн-школе Skysmart от Skyeng:

3. Законы Ньютона.

Следует подчеркнуть, что в условиях выбранных моделей применимы законы Ньютона.

4. Абсолютно твердое тело.

Модель абсолютно твердого тела также может быть применима при условии, что: тело обладает конечной массой, конечными размерами, а расстояние между двумя любыми точками тела неизменно. В обоснование это можно записать следующим образом:

• Применима модель твердого тела, так как расстояние между любыми двумя точками тела, его форма и размеры неизменны.

При этом, рассматривая модель абсолютно твердого тела, нужно указать, что:

• Движением твердого тела является совокупность поступательного и вращательного движений. Поэтому применимы условия равновесия твердого тела: для поступательного (второй закон Ньютона) и для вращательного движений (равенство моментов сил относительно выбранной оси).
• Применимы уравнения моментов и второго закона Ньютона.

Советуем посмотреть еще планы уроков по физике:

5. Нить. Блоки. Пружины.

В задачах с телами, связанными нитью, обязательно следует упомянуть о следующем: 

• Нить нерастяжима, поэтому ускорения связанных тел равны (при отсутствии блоков или неподвижном блоке).
• Нить нерастяжима, поэтому модули ускорений подвижного блока и тела при их поступательном движении отличаются в два раза.
• Нить невесома, поэтому модуль силы натяжения в любой точке нити одинаков. 

Если в задаче присутствует блок, то:

• Блок является идеальным, то есть его масса пренебрежимо мала, трение в блоке отсутствует.

Если в задаче присутствует пружина, то:

• Силы упругости на концах пружины одинаковы, так как пружину считаем невесомой (легкой).

6. Сила трения.

Если в задаче силой трения не пренебрегают, обязательно указать, какая именно это сила: трения покоя или трения скольжения.

7. Закон сохранения энергии (ЗСЭ).

Нужно обязательно определить систему тел и сформулировать условия для выполнения закона. Так как очень редки случаи, когда система замкнута, нужно объяснить, почему в данном случае закон сохранения применим. Обратите внимание: сказать, что «система замкнута», недостаточно. Поэтому придется указать силы, действующие на каждое тело, указать, какие из действующих сил являются непотенциальными, сформулировать ЗСЭ.

Например, в задаче про шарики на рис. 3, можно записать следующее:

• В процессе движения каждого шарика в верхней точке траектории на каждый из них действуют сила тяжести и сила натяжения нити. Изменение механической энергии шарика в ИСО равно работе всех непотенциальных сил, приложенных к нему. В данном случае единственной такой силой является сила натяжения нити. Однако в каждой точке траектории сила натяжения нити перпендикулярна скорости шарика, поэтому работа силы равна нулю, а механическая энергия каждого шарика на этом участке его движения сохраняется.

Таким образом, можно сказать, что ЗСЭ применим при наличии непотенциальных или внешних сил: например, силы реакции опоры или силы натяжения нити, так как они всегда перпендикулярны скорости тела, поэтому работа этих сил не совершается.

У нас есть и другие материалы по физике:

8. Закон сохранения импульса (ЗСИ).

При использовании ЗСИ необходимо учесть следующе параметры: 

• Проекции внешних сил на выбранную ось равны нулю.
• Внутренние силы много больше внешних (например, во время взрыва или соударения).
• Внешние силы скомпенсированы.

Например,

• Ось Ox сонаправим с начальной скоростью бруска. Система «брусок — кусок пластилина» является замкнутой, так как сумма проекций внешних сил (сила тяжести) на ось Ox равна нулю, а силы трения и сопротивления воздуха отсутствуют. Следовательно, можно применять закон сохранения импульса для данной системы тел при неупругом соударении, после которого тела становятся одним целым.

• Так как трением снаряда и осколков о воздух можно пренебречь, то для описания разрыва снаряда применим закон сохранения импульса системы тел. Однако внешняя сила тяжести не равна нулю, но ею можно пренебречь, считая время разрыва гранаты малым. За малое время разрыва импульс каждого из осколков меняется на конечную величину за счет больших внутренних сил, разрывающих снаряд при взрыве. По сравнению с этими силами сила тяжести пренебрежимо мала. Так как время разрыва гранаты считаем малым, то можно пренебречь и изменением потенциальной энергии гранаты и его осколков в поле тяжести в процессе разрыва. В инерциальной системе отсчета выполняются законы сохранения импульса и энергии с учетом энергии разрыва.

Часто выпускники даже не приступают к выполнению 26 задания — и очень зря. Несмотря на мнимую сложность, многие задания оказываются намного проще, чем могут показаться на первый взгляд. Прежде чем приступить к решению задания, важно хорошо понять его условие. Для успешного решения задач по физике на ЕГЭ важно иметь хорошее представление о физических законах и формулах. А главное — регулярно повторять материал и закреплять его практическими заданиями. Не сомневайтесь в своих знаниях и уверенно приступайте к решению. Успехов вам!