Разбор нашумевшего примера 36:3(8-6)/6 по математике
В соцсетях не первый год гуляет противоречивая математическая конструкция без знака умножения. Мнения о правильном решении этого примера разделились, существует два варианта ответа. Только появление в точных науках примеров с «неоднозначным» решением — это скорее исключения. И со временем исследования, обсуждения и дискуссии доводят это исключение до единственно верного ответа.
В этой статье разберем пример как раз из тех, где правильное решение только одно.
Станьте звездой онлайн-вебинаров по математике
Получайте от 100 000 ₽ за яркую
и увлекательную подготовку к ОГЭ и ЕГЭ 🔥
Важно: вы сдали ЕГЭ на высокий балл
Заполнить анкету
Содержание:
- Какие есть варианты решения
- Почему знак умножения опускается
- Как решается пример
- Почему пример 36:3(8-6)/6 некорректен
Какие есть варианты решения
У примера есть два ответа. Или нет — ответ в конце статьи!
| Для математиков начальных классов ответ — 4 | Для учеников средней школы ответ — 1 |
Если в примере указать знак умножения, тогда все становится однозначно: действия выполняются по порядку, результат равен 4.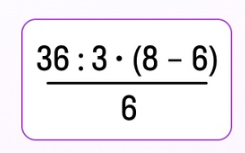 | В примере, который мы разбираем, знак умножения опущен. Из-за этого читать пример можно по-разному: либо нужно делить только на 3, либо нужно делить на произведение 3 и (8 – 6). |
Больше подробностей о преподавании математики у нас в статьях:
Почему знак умножения опускается
Первая причина — упростить запись. Это легко заметить в выражениях 2x, xy, abc, которые выглядят приятнее, чем 2 * х, x * y, a * b * c.
Вторая причина — показать, что перед нами один объект. Это хорошо иллюстрирует тема одночленов в математике 7-го класса. Например, 2abc — это одночлен в стандартном виде, а 2a * bc — это уже произведение двух одночленов, результатом которого станет выражение 2abc.
Рассмотрим выражение: 2х : 2х.
Здесь знаки умножения опущены не только для краткости. Благодаря этому мы видим частное одночленов, результатом которого становится 1.
Если бы перед нами было выражение 2 * х : 2 * х, то результат был бы х^2. Здесь сработали правила последовательного выполнения действий.
Третья причина — математики опускают знаки действий для краткости и красоты.
Рассмотрим пример, когда красота важнее правильной записи
В 8 классе школьники изучают основное тригонометрическое тождество sin2x + cos2x = 1. Эта запись полностью противоречит смыслу, который она несет. Такое использование квадрата подразумевает sin(sin(x)) — применение функции к самой себе.
Корректная запись была бы такой: (sin(x))2 + (cos(x))2 = 1.
Для простоты и красоты математики пошли на такой шаг с позицией, что их правильно поймут. И благодаря этому мы знаем основное тригонометрическое тождество в том виде, в котором его дают в школьных учебниках.
Как решается пример
Если пример подразумевает, что нужно выполнять действия последовательно, необходимо поставить знак умножения. С ним сложность записи не увеличивается, красота и понятность примера не теряются.
Так как знак умножения в исходном примере 36:3(8-6)/6 не указан, автор вкладывал в выражение другую последовательность действий.
Если же мы захотим строго записать пример, в котором нужно делить на все выражение 3(8–6), тогда его придется записать так:
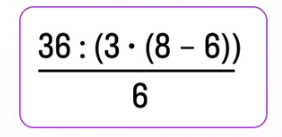
Пример теперь выглядит громоздко и неуклюже из-за двойных скобок. Поэтому для такого сценария вычислений будет корректна запись:
Знак умножения опущен для того, чтобы показать цельность двух объектов и чтобы не нагромождать выражение двойными скобками.
Почему пример 36:3(8-6)/6 некорректен
При создании учебников и литературы для знаков умножения действует правило: знак умножения опускается, если ошибка невозможна.
Речь идет о единственной интерпретации выражения. В примерах, которые мы приводили выше, ошибки не случаются — их понимают одинаково.
В примере 36:3(8-6)/6, который стал поводом для этого материала, случились разногласия.
Следовательно, знак умножения в данном случае опущен некорректно.
Добавить комментарий
Екатерина Ломакина 
Анна Михайлова-Левина 
Ирина Чегринская 
Мария Лазарева
Вы сами противоречите себе. Раз можно толковать по-разному, умножение опущено некорректно. Значит там должно быть умножение. И ответ 4. «Автор не хотел загромождать»…. Так к чему тогда глупое выражение (8-6)?Написал бы 2. И в этом случае тогда умножение.
Здесь как раз скобки излишни. Не влияют на результат
Господа авторы, вы заблуждаетесь. Утверждения: «автор вкладывал в выражение другую последовательность действий», «пример теперь выглядит громоздко и неуклюже из-за двойных скобок» — это ваше личное мнение, не имеющее ничего общего с арифметикой.
Ну и че за дичь этот интернет ваш. Начал искать ответ.
На первом сайте профессор математики доказал, что ответ четыре. Открываю второй сайт, ваш , в доказываете что один. И как жить то?
Можно ли рассматривать ответы инженерных калькуляторов, как довод в пользу утверждений изложенных в статье?
Как быть инженерными и научными калькуляторами, часть из них не берёт без знака умножения и тогда конечно 4. Но часть берёт и со знаком и без него. И тогда без знака получается 1, ну а со знаком 4. Показывают один и второй вариант…
Как быть с инженерными и научными калькуляторами, большая часть из них при опущенном знаке умножения показывает результат 1. А со знаком результат 4. Часть просто не берёт без знака.
А вот это что ? «36:3(8-6)/6». Ещё одна неоднозначность ? Тогда уж (36:3(8-6))/6
что бы получить 4 в решении этой дроби , она должна выглядеть так , числитель 36:3*(8-6)=24 , делим на знаменатель 6 тогда получаем 4, или переместим скобку так— 36*(8-6) :3 =24 , здесь показан знак умножения как математическое действие и здесь правило без приоритета «шуруй» слева на право —в приведенном примере математический знак умножения отсутствует это уже правило в старших кл. и в высшей математике показывают в примере целостную цифру , разбитую на несколько элементов и если это не целостная цифра то в примере обязательно пишут знак * умножение , для верного решения примера , для меня это как на «автомате» после «вышки» ,нет знака *значит значит это целая цифра 6 , если стоял бы знак * — 36:3*(8-6) , то решение таково—36:3=12 , (8-6)=2, 12*2=24 , затем на знаменатель 6=4 — НО В ПРИМЕРЕ 3(8-6) , ЗДЕСЬ ПРАВИЛО ЦЕЛОСТНОСТИ ОДНОЙ ЦИФРЫ 6 , КОТОРАЯ РАЗБИТА НА НЕСКОЛЬКО ЭЛЕМЕНТОВ с разными матем-ми действиями и решение здесь ===1.
,нет знака *значит… А ТО И ЗНАЧИТ ЧТО ТОТ КТО ЕГО УБРАЛ -МОШЕННИК-ТАК КАК ПРИ ОПУСКАНИЯ ЗНАКА *УМНОЖЕНИЕ С ДЕЛЕНИЕМ ПЕРЕД ЦИФРОЙ3 ОН НЕ ЗАВЕРШИЛ ДЕЙСТВИЕ- А ИМЕННО НЕ ЗАКЛЮЧИЛ ЦИФРУ3 В ДОПОЛНИТЕЛЬНУЮ СКОБКУ ЧТОБЫ ИСКЛЮЧИТЬ ДВОЙСТВЕННОСТЬ В ОЧЕРЕДНОСТИ ДЕЙСТВИЙ….ОТВЕТ- НЕ ПОСТАВИЛ СКОБКУ — ВЕРНИ ЗНАК*УМНОЖЕНИЕ
Попробуй раскрыть скобки d:а(b-c) По другому как d:аb-d:аc не получается… И если по твоему аb и аc это целые цифры (ведь там не стоит знак умножения, а только подразумевается), то ответ в данном примере вообще получится отрицательный. Поэтому не надо к простому примеру приплетать высшую математику — ответ однозначно 4.